Problema: Snakes and Ladder

A cada rodada um jogador joga uma moeda não viciada avança 1 casa se obtiver cara ou avança 2 casas se obtiver coroa. Se o jogador para no pé da escada, então ele imediatamente sobe para o topo da escada. Se o jogador cai na boca de um cobra então ele imediatamente escorrega para o rabo. O jogador sempre inicia no quadrado de número 1. O jogo termina quando ele atinge o quadrado de número 36.

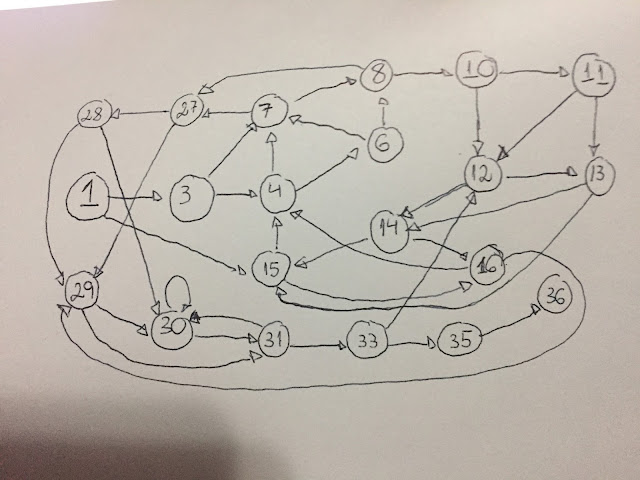
Diagrama de estados obtido para esse caso (Vale lembrar que alguns estados foram omitidos já que eles ou tem escada ou tem a cobra e na regra do jogo acabam nem ficando nesse estado):

* Todas as arestas desse grafo possuem peso 1/2

A matriz de transição de estados é mostrada na imagem abaixo (Nesta matriz os estados não foram omitidos como no diagrama de cima):

Agora para usarmos o power method foi feito este algoritmo em python:

Temos o vértice 1 como inicial, e isso pode ser observado na lista ini.
A partir disso fazemos uma multiplicação de matrizes na função calculoDist e para ter resultados em tempos diferentes foi usado a função tempoCalc.

Aqui um exemplo da saída nos primeiros passos:

Ao fim do passo 100 que foi considerado encontramos que a maior probabilidade é de estar no estado 30 (probabilidade de 0.011 aproximadamente) e a chance de ganhar o jogo, ou seja, estar no estado 36 é de 0.003 aproximadamente.

Algoritmo de Prim

Este algoritmo é usada para gerar as chamadas Minimal Spanning Tree (MST). Para falarmos mais disso primeiramente vamos definir o que é uma árvore.
- G é um grafo;
- G é acíclico se não contém ciclos;
- G é uma árvore se for acíclico e conexo.

Para este algoritmo vale lembrar que é preciso um grafo que contenha peso nas arestas (grafo ponderado). Encontrar uma MST consiste que se escolha um vértice inicial, em cada passo se escolha uma aresta de menor peso, que respeite a regra de não formar ciclos, até passar por todos os vértices.
Embaixo temos uma imagem que representa como o algoritmo funciona.

Então para que esse algoritmo seja feito primeiro vamos usar uma primitiva que pega o menor valor de um conjunto:

Agora o algoritmo implementado:

Na linha 64, 65, 66 e 67 é onde ocorre a lógica principal do algoritmo que verifica se o valor de um vértice é maior que a aresta que estamos observando para atingir este mesmo nó. Se for maior que dizer que compensa ir na aresta porque queremos o menor valor.
Abaixo temos uma foto que mostra o resultado obtido quando usamos este algoritmo.

Fontes e ferramentas:

https://pt.wikipedia.org/wiki/Algoritmo_de_Prim;
https://www.ime.usp.br/~pf/algoritmos_para_grafos/aulas/prim.html;

Notas de aula da matéria;

Python(x,y);

Spyder Python.

Algoritmo Djikstra

Esse tutorial tem como objetivo passar uma noção do algoritmo de Dijkstra e também algumas observações a serem feitas. Ele sempre encontra o melhor caminho e é muito parecido com um algoritmo já visto no blog, o algoritmo de Prim.
A diferença entre o de Prim e Dijkstra é a operação de relaxamento nas arestas (primitiva relax), que verifica se é possível diminuir o custo do caminho até o vértice. O Algoritmo de Djikstra soluciona o problema do caminho mais curto num dado grafo. Iniciando em um vértice raiz, logo esse tem custo 0, olhando agora para as adjacências ele escolhe aquelas que tiverem menor custo para atingir o vértice, ou seja, é necessário olhar para um custo já calculado + peso da aresta (onde difere de Prim) e comparar com o custo existente no vértice que deseja chegar. Para isso utilizamos de algumas primitivas que são a relax e extractMin.

Lembrando que antes era necessário ler de um arquivo específico os nossos dados, que foi feito nesta parte do código:

Agora que já temos o nosso grafo e também as nossas primitivas que são usadas no algoritmo, implementamos ele:

Note o uso das primitivas nas linhas 70 e 76.
O seu segundo argumento S, é usado para nosso K (vértices que terão custo 0 inicialmente) e veremos mais a frente o porque isso foi usado.
Agora quando esse algoritmo foi executado no nosso grafo, obtivemos este resultado:

Este grafo acima foi usado um conjunto K = 1, ou seja, apenas o vértice raiz tinha custo como 0. Isso implica que no grafo existirá apenas um grupo de vértices, se mudarmos esse valor teremos novos resultados. A seguir aplicamos K = 2 e K = 3 respectivamente a fim de observar o que aconteceria no crescimento do grafo.

Os vértices com custo 0 nesse grafo a cima foram os vértices 29 e 102. É possível observar no grafo que eles fazem partes de comunidades diferentes. Como aqui o K=2 temos 2 grupos distintos de vértices, chamamos de comunidade.
Já na figura abaixo temos K=3 com os vértices que iniciaram seu custo em zero sendo 64, 88 e 125.

Fontes e ferramentas:

https://pt.wikipedia.org/wiki/Algoritmo_de_Dijkstra;

https://passeiemgrafos.wordpress.com/;

Notas de aula da matéria;

Python(x,y);

Spyder Python.